Mit Nutzung dieser Website stimmen Sie der Verwendung von Cookies zu. Mehr erfahren
 
Der Betrieb und die Weiterentwicklung dieser Internetseite wird durch Werbung ermöglicht. Bitte deaktivieren Sie Ihren Adblocker.
Im Firefox dazu einfach auf das (i) in der Adressleiste klicken und "Blockieren temporär deaktivieren" auswählen.
Sinuswellen - Grundlagen der Mathematik
Startseite · Analysis · Finanzmathematik · Übungen · Bruchtrainer · Glossar · Kontakt

Analysis

1. Differentialrechnung

1.3. Anwendungen

1.3.4. Newton-Verfahren

Das Newton-Verfahren nutzt die Differentialrechnung um Nullstellen von Funktionen näherungsweise zu bestimmen. Dies ist immer dann notwendig, wenn die Nullstellen nicht direkt berechnet werden können oder die Berechnung zu aufwendig wäre.

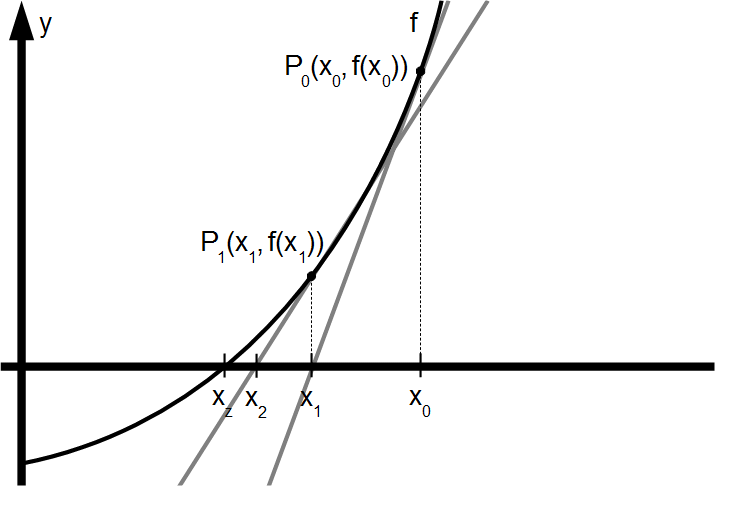
Wie das Newton-Verfahren funktioniert ist in Abbildung 1.11. dargestellt. Gegeben sei dazu eine Funktion f für die eine Nullstelle xz ermittelt werden soll. Zunächst wählt man einen Startwert x0 und berechnet die Nullstelle der Tangenten durch den Punkt P0(x0, f(x0)). Die Tangente hat bei x1 eine Nullstelle, dieser Wert liegt normalerweise deutlich näher am gesuchten Wert xz. Nun berechnet man die Nullstelle der Tangenten durch den Punkt P1(x1, f(x1)) und erhält x2 , usw.

Bild: Newton-Verfahren
Abb. 1.11. Newton-Verfahren

Die Formel zur Berechnung der jeweiligen Werte lautet:

xn+1 =  xn -  f(xn)
f '(xn)

Es handelt sich also um ein iteratives Verfahren, d.h. mit jeder Wiederholung kommt man der tatsächlichen Lösung normalerweise immer näher. Daher muss eine Bedingung festgelegt werden, wann der errechnete Wert hinreichend genau ist und die Berechnung beendet werden kann. In der Praxis wird das Verfahren meist abgebrochen, wenn sich eine vorher festgelegte Nachkommastelle über 2 Iterationsschritte hinweg nicht mehr ändert.

Beweis

Um die Formel für das Newton-Verfahren herzuleiten stellen wir zunächst die Geradengleichung für die Tangente an einem Punkt Pn(xn, f(xn)) auf. Allgemein lautet die Geradengleichung:

y = m⋅x + n

Dabei bezeichnet m die Steigung der Geraden und n den y-Wert an dem die Gerade die y-Achse schneidet. Da es sich um eine Tangente an dem Punkt Pn handeln soll, muss die Steigung der 1. Ableitung der Funktion entsprechen und es gilt somit m = f '(xn). Zusammen mit Koordinaten des Punktes Pn setzen wir dies in die Formel ein, um n zu bestimmen.

f(xn)  =  f '(xn)⋅xn + n
n  =  f(xn) - f '(xn)⋅xn

Die Geradengleichung für die Tangente lautet demnach:

y = f '(xn)⋅x + f(xn) - f '(xn)⋅xn

Der nachfolgende Wert xn+1 ist Nullstelle der Tangente, somit gilt dafür y = 0.

0 = f '(xn)⋅xn+1 + f(xn) - f '(xn)⋅xn

Man muss die Gleichung nur noch nach xn+1 (mit f '(xn) ≠ 0) umformen und erhält die Formel für das Newton-Verfahren.

f '(xn)⋅xn+1  =  f '(xn) ⋅xn - f(xn)
xn+1  =  xn -  f(xn)
f '(xn)
Beispiel

Es soll eine Nullstelle der Funktion f(x) = x3 - 0,3x2 + 5x - 1,5 mit dem Newton-Verfahren näherungsweise bestimmt werden.Die Iteration soll beendet werden, sobald sich die 2. Nachkommastelle nicht mehr ändert.

Zunächst benötigen wir die 1. Ableitung der Funktion, diese muss nur einmalig berechnet werden. Für die Berechnung der Ableitung wird auf die Methoden aus Kapitel 1.2. verwiesen.

f '(x) = 3x2 - 0,6x + 5

Als nächstes muss ein Startwert gefunden werden. Dafür gibt es viele Möglichkeiten, die einfachste ist es zu raten. Wir probieren es mit x0 = 1. Für x1 ergibt sich durch Anwendung der Formel:

x1 =  x0 -  f(x0)  =  1 -  13 - 0,3⋅12 + 5⋅1 - 1,5  ≈  0,4324
f '(x0) 3⋅12 - 0,6⋅1 + 5

Nun verwenden wir x1 = 0,4324 um den nächsten Näherungswert x2 zu berechnen, usw.

x2 =  x1 -  f(x1)  =  0,4324 -  0,6868  ≈  0,3029
f '(x1) 5,3015
x3 =  x2 -  f(x2)  =  0,3029 -  0,0148  ≈  0,3000
f '(x2) 5,0935

Die Iteration wurde nun beendet, da sich die 2. Nachkommastelle nicht mehr verändert hat. Durch Einsetzen in die Funktion stellt man fest, dass x3 = 0,3 sogar der exakte Wert der Nullstelle ist.

Übungen
  1. Es soll eine Nullstelle der Funktion f(x) = x3 - 1,5x2 + 2x - 3 mit dem Newton-Verfahren näherungsweise bestimmt werden.
    Die Iteration soll beendet werden, sobald sich die 2. Nachkommastelle nicht mehr ändert.
    Die Zwischenergebnisse können auf 4 Nachkommastellen gerundet werden.
    Als Startwert soll x0 = 1 verwendet werden.
  1. Um die Wurzel aus 2 näherungsweise zu berechnen, soll eine Nullstelle der Funktion f(x) = 2 - x2 mit dem Newton-Verfahren näherungsweise bestimmt werden.
    Die Iteration soll beendet werden, sobald sich die 2. Nachkommastelle nicht mehr ändert.
    Die Zwischenergebnisse können auf 4 Nachkommastellen gerundet werden.
    Als Startwert soll x0 = 2 verwendet werden.

Übungsaufgaben und Lösungen

Alle Angaben ohne Gewähr